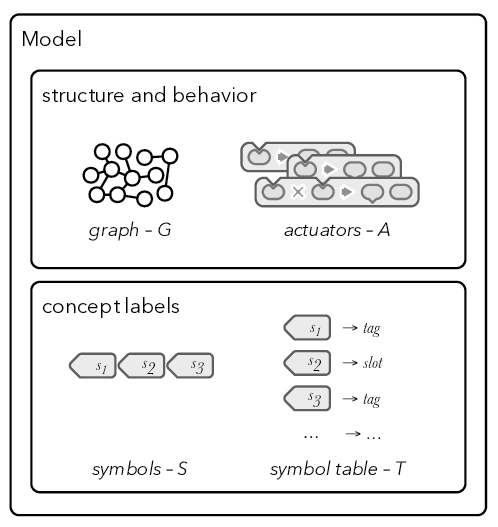
Model
The modeled universe comprises of a system’s state and description of the system’s dynamics. The state is a graph where we call nodes objects which have qualitative properties associated with them. The system’s dynamics is a collection of rules describing system’s behavior called actuators.
To be able to refer to particular components of the model in a human readable form we use symbols. Each symbol can refer to either particular component of the model or a type of component.
- Definition
Model is a tuple \(M:=(S, S\rightarrow t, A, G)\) where \(S\) is a set of symbols, \(S\rightarrow t\) is a symbol type table where \(t\) is a symbol type, \(A\) is a collection of actuators and \(G\) is a graph representing system’s state.
- Definition
Symbol table \(S\rightarrow t\) is a mapping between a symbol and it’s type: \[T:=s\rightarrow t|s\in{S},t=\begin{cases}\text{tag}\\\text{slot}\\\text{actuator}\end{cases}\] We say that a symbol \(s^t\) is of type \(t\) when \(s^t\in{S}\wedge T(s^t)=t\). Set of symbols \(S^t\) is a set where each symbol is of type \(t\).
Object is indivisible entity representing an instance of relevant concept within simulated universe. It is a carrier of qualitative properties - tags. State of an object is denoted by a set of tags.
- Definition
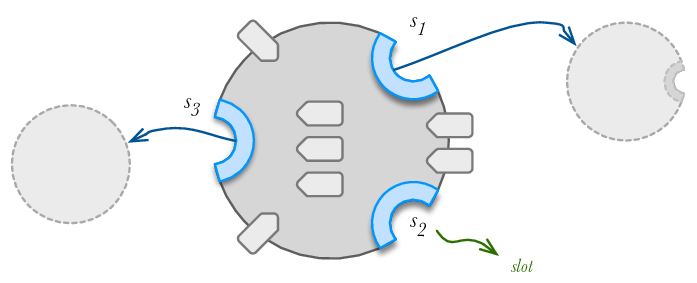
Object graph \(G\) is labeled oriented multigraph of objects (edges) and relationships (vertices) \((O,R)\). Relationship is a tuple \(\{s^\text{slot},o\}\) where \(s^\text{slot}\in S\) and \(o\in O\)
- Definition
Object’s qualitative state is a set of symbols \(\{s^t_1, s^t_2, ..., s^t_n\} | s^t_i \in S^\text{tag}\). We will write it as \(\text{tags}(o)\)
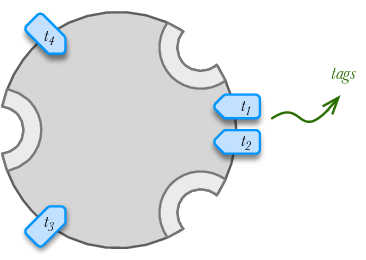
Slot is a relational property of an objects that references other objects. Slot is a label of an edge of the object graph. We will use the letter \(s\) to denote a slot.
- Proposition
We say that object \(o\) has slots \(\{s^s_1, s^s_2, ..., s^s_n\}\) if there exist edges \(\{o,s^s_i\}\). We will write it as \(\text{slots}(o)\)
Before we proceed with the system’s dynamics, we need to define one more design concept of the system: local context.
- Definition
Local context of an object \(o\) is a subgraph \(G^L\subseteq G\) with all objects and relationships where object \(o\) is the inital vertex.
In other words, local conetxt of an object \(o\) is a subgraph within a graph distance of 1 from the object \(o\).
Before we move on with defition of other concepts, we need to define how objects in the graph can be reffered to. We need to be able to refer to an object within the local context relatively to the object being considered for evalutaion.
- Definition
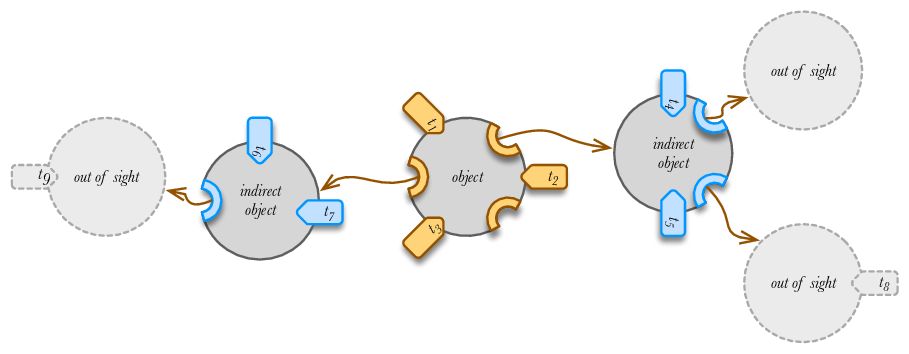
Subject mode is a relative reference to an object in the graph given initial object. \[m:=\begin{cases}\text{direct}\\\text{indirect}(s^\text{slot})\end{cases}\]
Subject mode is used to determine which object will be used for pattern matching in the selector or for applying state transitions. We call the object that is to be used for evaluation effective subject. Direct subject mode means that the effective subject is the object being evaluated is to be considered. Indirect subject mode means that the effective subject is the object which is terminal vertex \(o_t\) of the relationship \(\{s^\text{slot},o_t\}\) where the initial vertex is the object being evaluated.
Model Dynamics
The main concepts for the model dynamics are:
- Actuator is a description of an atomic state transition of objects within the graph matching a pattern.
- Selector is a match pattern or objects subject to transition
- Transition/Modifier is a description of state change affects either object’s state or local relationships
Pattern matching or state transitions can happen only within a local context. The local context is an intentional design limitation which restricts that object state and graph transitions can happen only within distance of 1 from the selected object. Assumption here is that if we want to reach an object with larger distance we have to use multiple steps and therefore be open for interference - which is desired by design.
Actuators
Actuators can be thought as declarations of graph rewrite rules combined with object state transitions. They are applied to the whole graph1. We assume that all actuators operate on all objects at once.2
The graph can be modified either through a state of a single object or a state of two object in their hypothetical interaction.
For observation and controlled simulation purposes the actuators have also a control signallig associated with them. We will discuss the control mechanism later.
Unary Actuator describes transition of object’s state and local relationships based on previous object’s state. Only object that matches a pattern or it’s direct neighbours can be affected.
Binary Actuator is a conditioned transition of an object as a result of cartesian product of two objects matching two selector patterns. Either of two objects can undergo transition based on state of any of the objects in the cartesian product tuple.
- Definition
Unary actuator is a tuple \((\sigma, m\rightarrow T^1, n)\) where \(\sigma\) is a selector, \(m\) is subject mode and \(T^1\) is unary transition. \(n\) is a control signal (as in “notification”).

Binary actuator is the only way how a new connections to potentially unrelated objects (no direct reference) might happen.
- Definition
Binary actuator is a tuple \((\sigma_l, \sigma_r, m_l\rightarrow T^2_l, m_r\rightarrow T^2_r, \Gamma)\) where \(\sigma_l\) and \(\sigma_r\) are left and right selector respectively, \(T^2_l\) and \(T^2_r\) are left and right binary transitions on effective subject specified by left subject mode \(m_l\) and right subject mode \(m_r\) respectively. \(n\) is a control signal.
We would use the term hand to refer to the left or right selector or transition.
Model language declaration of a binary actuator is:
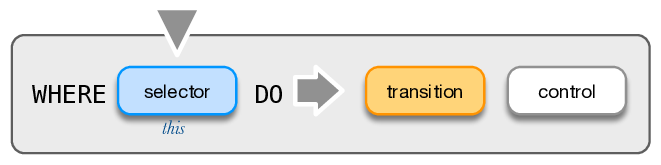
REACT actuator_name
WHERE (selector_patterns)
ON (selector_patterns)
DO binary_transitionsSelector
Selector is a pattern description that matches properties of objects and their local context. Pattern is a collection of multiple predicates that test qualitative properties or existence of relationships of an object. An object matches a selector pattern when:
- a direct predicate matches the object
- an indirect predicate matches object’s direct neighbors
The predicates can tets for:
- Tags associated with an object: true if \(\text{selector's tags}\subset\text{object’s tags}\)
- Tags not associated with an object: true if \(\text{object’s tags}\cap\text{selector’s tags}=\emptyset\)
- Graph contains an edge from a specific slot
- Graph does not contain an edge from a specific slot
- Definition
Selector is a patter description \[\sigma:=\begin{cases}\text{all}\\\text{match}(m\rightarrow \Pi)\end{cases}\] where \(m\) is a subject mode and \(\Pi\) is a selector pattern. We say that object matches a selector when the selector is \(\text{all}\) or when the effective subjects of the object match all the selector patterns \(\Pi\).
- Definition
Symbol presence \(p\) is a case \[p:=\begin{cases}\text{present}\\\text{absent}\end{cases}\].
- Definition
Selector pattern \(\Pi\) is a tuple of mappings \((S^t\rightarrow p, S^s\rightarrow p)\) where \(p\) is symbol’s presence. An object matches the selector pattern if all of the following are true: \[ \begin{aligned} & \ \{s^t|s^t\rightarrow \text{present}\} \subset \text{tags}(o) \\ \wedge & \ \text{tags}(o) \cap \{s^t|s^t\rightarrow \text{absent}\}=\emptyset \\ \wedge & \ \{s^s|s^s\rightarrow \text{present}\} \subset \text{slots}(o) \\ \wedge & \ \text{slots}(o) \cap \{s^s|s^s\rightarrow \text{absent}\}=\emptyset\end{aligned} \]
The language representation of the selector pattern is either a word ALL or a list of symbols. Assume we have symbols open, empty referring to tags and symbol next referring to a slot. For example the selector in the following actuator matches all objects that have tag open set, have no empty tag set and there exists a relationship at slot next from the object:
WHERE (open, !empty, next) ...All symbols are considered to be in direct subject mode by default. Indirect subject mode in the selector can be represented by object qualifier “dot” operator as indirection.symbol3. For example:
WHERE next.open ...The above matches an object where an object referred through slot next has a tag open set.
State Transitions
State transitions (further just transitions) are descriptions of qualitative changes of the object graph. They operate on objects and their neighbors within their local context. Proposed transitions are non-divisable primitives we assume being sufficient for any desired graph state transformations when composition of the transitions is used.
The concrete object that is subject to transition is called effective subject of the transition and is determined by the subject mode in the actuator.
There are two kinds of transitions: qualitative state of an object and qualitative state of the graph. The first one operates on object’s qualitative properties - tags and the later operates on graph’s relationships. The tags can be associated or disassociated from an object. The relationships can be bound and unbound within the local context of the effective subject.
Unary Transition
- Definition
Unary transition is a tuple \(T^1=(S^\text{tag}\rightarrow p,S^\text{slot}\rightarrow \mu^1)\) where the first element is a qualitative transition of the effective subject and the second element is a graph edge change from the effective subject to effective target as described by the unary target specifier \(\mu^1\).
If the \(p = \text{present}\) then the \(S^\text{tag}\) is associated with the effective subject. If the \(p = \text{absent}\) then the \(S^\text{tag}\) is dissociated with the effective subject. 4
- Definition
Unary target specifier \(\mu^1\) is a case: \[ \mu^1:=\begin{cases} \text{unbind}\\ \text{subject}\\ \text{in\_subject}(S^\text{slot})\\ \text{indirect}(S^\text{slot},S^\text{slot})\\ \end{cases}\] The \(\text{unbind}\) case specifies that the edge from the effective subject is to be removed. \(\text{subject}\) denotes that the target is the effective subject itself, therefore creating a self-loop. Effective target of the \(\text{in\_subject}\) case is the object referred by the specified slot from the effective subject. The \(\text{indirect}\) effective target is an object reffered to by the path of two slots from the effective subject.
The above gives us the following potential subject mode combinations for creating an edge using unary actuator. Let’s assume the effective subject having slots \(s\) and \(t\), and the object referred to by slot \(s\) having slot \(i\), object referred to by slot \(t\) having slot \(w\).
| Effective subject | Effective target | Edge |
|---|---|---|
| \(\text{direct}\) | \(\text{none}\) | removed |
| \(\text{direct}\) | \(\text{subject}\) | \(s\rightarrow \text{self}\) |
| \(\text{direct}\) | \(\text{in\_subject}(t)\) | \(s\rightarrow t\) |
| \(\text{direct}\) | \(\text{indirect}(t, w)\) | \(s\rightarrow t.w\) |
| \(\text{indirect}(i)\) | \(\text{none}\) | removed |
| \(\text{indirect}(i)\) | \(\text{subject}\) | \(s.i\rightarrow \text{self}\) |
| \(\text{indirect}(i)\) | \(\text{in\_subject}(t)\) | \(s.i\rightarrow t\) |
| \(\text{indirect}(i)\) | \(\text{indirect}(t, w)\) | not atomic |
- Constraint
Indirection of effective subject and effective target is not permitted, as the operation can be achieved by by composing two separate actuators: one for pulling indirect object closer to the effective subject and second for performing indirect bind to the pulled-in subject and unbinding the subject.
Binary Transition
Binary transition is analogous to the unary transition with one difference: the effective target specifier can specify one of the two “hands” of the selector.
Effective subject of the binary transition is the subject selected by corresponding hand selector. For the left hand selector \(\sigma_l\) the corresponding transition is \(T^2l\) and the effective subject of the transition is the subject determined by \(\sigma_l\). Analogously for the right hand transition the effective subject is determined by the \(\sigma_r\).
Transition hand can affect only qualities of the effective subject on the same hand similarly to unary transition. Although transition hand can have effective target from the same hand or from the other hand. This allows us to create new relationships between objects that are from disconnected parts of the graph. We refer to the effective subject from the other selector simply as \(\text{other}\).
- Definition
Binary transition is a tuple \(T^1=(S^\text{tag}\rightarrow p,S^\text{slot}\rightarrow \mu^2)\) where the first element is a qualitative transition of the effective subject and the second element is a graph edge change from the effective subject to effective target as described by the binary target specifier \(\mu^2\).
The first element of the tuple for tags is the same as the mapping in the unary transition.
- Definition
Binary target specifier \(\mu^2\) is a case: \[\mu^1:=\begin{cases} \text{unbind}\\ \text{other}\\ \text{in\_other}(S^\text{slot})\\ \end{cases}\] The \(\text{unbind}\) case specifies that the edge from the effective subject is to be removed. \(\text{other}\) denotes that the target is the effective subject of the other hand. Effective target of the \(\text{in\_other}\) case is the object referred by the specified slot from the other hand’s effective subject.
Note that there is no indirection in the binary transition as it can be achieved by composing multiple transitions. Neither there is possibility to create binding within the same effective subject as it can be achieved by composing as well 5.
The following table lists allsubject mode combinations for creating an edge between objects in the binary actuator. Let’s assume the effective subject on one hand having slots \(s\) and \(i\), and the effective subject on the other hand having slot \(t\).
| Effective subject | Effective target | Edge |
|---|---|---|
| \(\text{direct}\) | \(\text{none}\) | removed |
| \(\text{direct}\) | \(\text{other}\) | \(s\rightarrow \text{other}\) |
| \(\text{direct}\) | \(\text{in\_other}(t)\) | \(s\rightarrow \text{other}.t\) |
| \(\text{indirect}(i)\) | \(\text{none}\) | removed |
| \(\text{indirect}(i)\) | \(\text{other}\) | \(s.i\rightarrow \text{other}\) |
| \(\text{indirect}(i)\) | \(\text{in\_other}(t)\) | \(s.i\rightarrow \text{other}.t\) |
Transition Modes Summary
The following figure shows all possible graph transitions for edge creation for both unary and binary actuators:
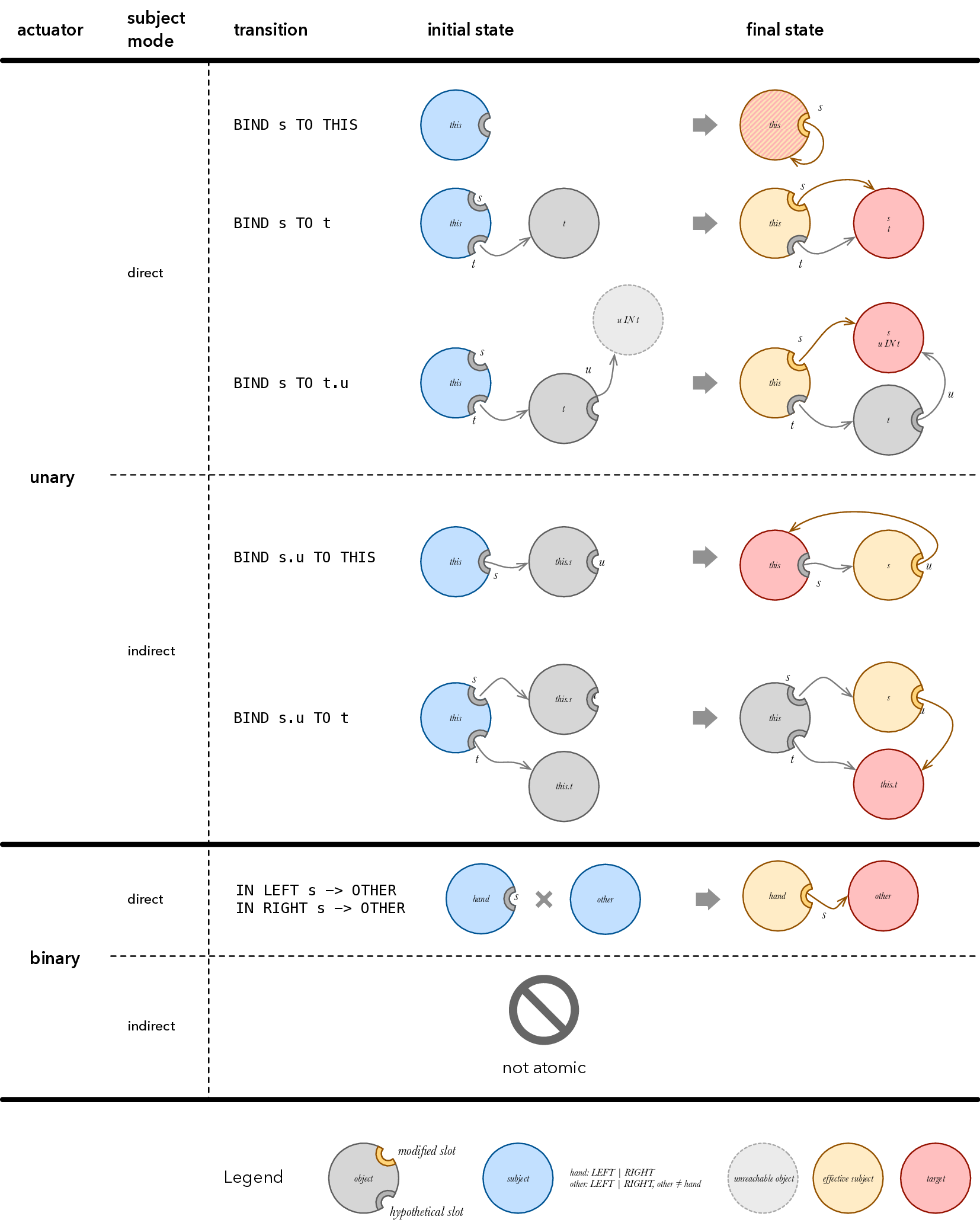
Binary modifier have limited ability to modify the state by design. Unbinding in a binary modifier can be achieved by a combination of binary state change and an unary UNBIND modifier. Indirection in the binary modifier can be achieved by a combination of binary direct subject state change and an unary modifier.
Note that all state changes beyond distance of 1 from the selected object must be composed of multiple transitions that propagate through the network. Susceptibility to being affected by other actuators along the way is intended design feature.
Here we assume only lowest level of the Sepro model without a constraints level. Higher levels as well as constraints are out of scope of this article.↩
This is idealized assumption which has technical implementation limitations that we will discuss later.↩
Unlike in common general purpose programming languages, the indirection can not be chained as in
deep.deeper.deepest.symboldue to the local context constraint.↩Alternative and more readable or understandable way of specifying which tags are to be associated or disassociated with an object would be to use two sets of tags: set and unset. However if the intersection of the sets is non-empty, the behaviour would be undefined. Using the mapping we prevent such situation from happening by design.↩
This is a design decision that we are proposing at this stage of system’s evolution. We have no firm opinion whether bindings within the same hand should be allowed or not at this moment.↩